Tree

树的定义:

有节点间的层次关系，分为父节点和子节点。
有唯一一个根节点，该根节点没有父节点。
除了根节点，每个节点有且只有一个父节点。
每一个节点本身以及它的后代也是一棵树，是一个递归的结构。
没有后代的节点称为叶子节点，没有节点的树称为空树。

树根据儿子节点的多寡，有二叉树，三叉树，四叉树等，我们这里主要介绍二叉树。

Binary tree

特殊的树，二叉树:

二叉树：每个节点最多只有两个儿子节点的树。
满二叉树：叶子节点与叶子节点之间的高度差为 0 的二叉树，即整棵树是满的，树呈满三角形结构。在国外的定义，非叶子节点儿子都是满的树就是满二叉树。我们以国内为准。
完全二叉树：完全二叉树是由满二叉树而引出来的，设二叉树的深度为 k，除第 k 层外，其他各层的节点数都达到最大值，且第 k 层所有的节点都连续集中在最左边。

二叉树的数学特征:

高度为 h≥0 的二叉树至少有 h+1 个结点，比如最不平衡的二叉树就是退化的线性链表结构，所有的节点都只有左儿子节点，或者所有的节点都只有右儿子节点。
高度为 h≥0 的二叉树至多有 2^h+1 个节点，比如这棵树是满二叉树。
含有 n≥1 个结点的二叉树的高度至多为 n-1，由 1 退化的线性链表可以反推。
含有 n≥1 个结点的二叉树的高度至少为 logn，由 2 满二叉树可以反推。
在二叉树的第 i 层，至多有 2^(i-1) 个节点，比如该层是满的。

二叉树的定义:

// Node 定义二叉树的节点
type Node struct {
    data  int
    left  *Node
    right *Node
}

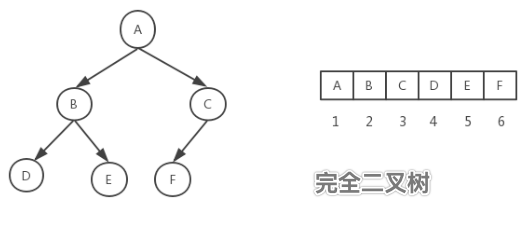
当然，数组也可以用来表示二叉树，一般用来表示完全二叉树。

对于一棵有 n 个节点的完全二叉树，从上到下，从左到右进行序号编号，对于任一个节点，编号 i=0 表示树根节点，编号 i 的节点的左右儿子节点编号分别为：2i+1,2i+2，父亲节点编号为：i/2，整除操作去掉小数。

在对树进行操作时，使用了大量的递归操作，这让代码变得优雅，但逻辑变得复杂，需要大量的画图才能理解。

插入节点

// 生成一个节点并返回它的地址
func getNewNode(n int) *Node {
    return &Node{data: n}
}

// Insert 在二叉树中插入一个节点
func (r *Node) Insert(n int) *Node {
    if r == nil {
        r = getNewNode(n)
    } else if n > r.data {
        r.right = r.right.Insert(n)
    } else {
        r.left = r.left.Insert(n)
    }
    return r
}

查找节点

// FindMini 查找树中的最小值
func (r *Node) FindMini() int {
    if r == nil {
        return -1
    } else if r.left == nil {
        return r.data
    }
    return r.left.FindMini()
}

func (r *Node) Find(n int) *Node {
    if r == nil {
        return r
    }
    if r.data == n {
        return r
    } else if r.data < n {
        return r.right.Find(n)
    } else {
        return r.left.Find(n)
    }
}

// FindMax 查找树中的最大值
func (r *Node) FindMax() int {
    if r == nil {
        return -1
    } else if r.right == nil {
        return r.data
    }
    return r.right.FindMax()
}

查找二叉树的高度

// FindHeight 查找二叉树的高度
func (r *Node) FindHeight() int {
    // height 指当前节点到最远叶子节点的边数量，叶子节点高度为0
    // depth 指从根节点到当前节点的边数，根节点深度为0
    if r == nil {
        return -1
    }
    // 画图理解
    return max(r.left.FindHeight(), r.right.FindHeight()) + 1
}

遍历二叉树

构建一棵树后，我们希望遍历它，有四种遍历方法：

先序遍历：先访问根节点，再访问左子树，最后访问右子树。
后序遍历：先访问左子树，再访问右子树，最后访问根节点。
中序遍历：先访问左子树，再访问根节点，最后访问右子树。
层次遍历：每一层从左到右访问每一个节点。

在计算机进行加减乘除等数学运算时，常常会使用数据结构来存储数值和符号，而后采用对应的遍历方式进行逐一计算，遍历出的计算顺序与实际的表达式顺序完全一致。

前序中序后序:

//L: left 左
//D: data 数据
//R: right 右


// Preorder 前序遍历 DLR
func (r *Node) Preorder() {
    if r == nil {
        return
    }
    println(r.data)
    r.left.Preorder()
    r.right.Preorder()
}

// Inorder 中序遍历 LDR
func (r *Node) Inorder() {
    if r == nil {
        return
    }
    r.left.Inorder()
    println(r.data)
    r.right.Inorder()
}

// Postorder 后续遍历 LRD
func (r *Node) Postorder() {
    if r == nil {
        return
    }
    r.left.Postorder()
    r.right.Postorder()
    println(r.data)
}

层级遍历:

又叫广度遍历，需要借助Queue配合使用

先将树的根节点放入队列。
从队列里面 remove 出节点，先打印节点值，如果该节点有左子树节点，左子树入栈，如果有右子树节点，右子树入栈。
重复2，直到队列里面没有元素。

// LevelOrder 层级遍历
func (r *Node) LevelOrder() {
    if r == nil {
        return
    }

    Queue := queue{} // 创建队列
    Queue.push(r) // 节点入栈

    for Queue.Size != 0 {
        v := Queue.pop() // 节点出栈

        println(v.data) // 打印节点值
        if v.left != nil {
            Queue.push(v.left) // 左子节点入栈
        }
        if v.right != nil {
            Queue.push(v.right) // 右子节点入栈
        }
    }
}

判断是否为二叉搜索树

完全递归方式，每个节点递归判断一次，代价为O( \(n^2\) )不推荐:

// IsSubtreeLesser 将当前节点值、所有子节点值与调用者传入的父节点值比较，如果任意节点大于父节点则返回 false
func (r *Node) IsSubtreeLesser(n int) bool {
    if r == nil {
        return true
    }
    if r.data < n &&
        r.left.IsSubtreeLesser(n) &&
        r.right.IsSubtreeLesser(n) {
        return true
    } else {
        return false
    }
}

// IsSubtreeGreater 将当前节点值、所有子节点值与调用者传入的父节点值比较，如果任意节点小于父节点则返回 false
func (r *Node) IsSubtreeGreater(n int) bool {
    if r == nil {
        return true
    }
    if r.data > n &&
        r.left.IsSubtreeGreater(n) &&
        r.right.IsSubtreeGreater(n) {
        return true
    } else {
        return false
    }
}

// IsBinarySearchTree 确定当前是否为二叉搜索树
func (r *Node) IsBinarySearchTree() bool {
    if r == nil {
        return true
    }
    if r.left.IsSubtreeLesser(r.data) &&
        r.right.IsSubtreeGreater(r.data) &&
        r.left.IsBinarySearchTree() &&
        r.right.IsBinarySearchTree() {
        return true
    } else {
        return false
    }
}

上下限比较法:

// IsBinarySearchTreeUtil 确定当前是否为二叉搜索树
func (r *Node) IsBinarySearchTreeUtil(miniValue, maxValue int) bool {
    // 这种方式给每个节点设置一个上下限，初始值为无穷，由于每种数据类型都是有长度的，所以这里取当前类型的极限值
    if r == nil {
        return true
    }
    if r.data < maxValue &&
        r.data > miniValue &&
        // 将最大值和最小值传递给下面的节点进行判断
        r.left.IsBinarySearchTreeUtil(miniValue, r.data) &&
        r.right.IsBinarySearchTreeUtil(r.data, maxValue) {
        return true
    } else {
        return false
    }
}

func (r *Node) IsBinarySearchTree() bool {
    return r.IsBinarySearchTreeUtil(math.MinInt, math.MaxInt)
}

删除节点

func (r *Node) Delete(n int) *Node {
    // 空树直接返回
    if r == nil {
        return r
        // 如果n在左边
    } else if r.data > n {
        r.left = r.left.Delete(n)
        // 如果n在右边
    } else if r.data < n {
        r.right = r.right.Delete(n)
        // 如果n在当前节点
    } else {
        // 如果当前节点没有子节点 直接置空
        if r.left == nil && r.right == nil {
            return nil
            // 如果当前节点没有左节点 返回右节点 即将当前节点替换为当前节点的右子节点
        } else if r.left == nil {
            return r.right
            // 如果当前节点没有右节点 返回左节点 即将当前节点替换为当前节点的左子节点
        } else if r.right == nil {
            return r.left
            // 如果两个子节点都有 则查找出最小的右子节点值 将当前节点值替换为该值 最后删除最小子节点
            // 因为右边的最小子节点一定比左边的节点大 所以替换当前节点没问题
        } else {
            temp := r.right.FindMini()
            r.data = temp
            r.right = r.right.Delete(temp)
        }
    }
    return r
}

查找中序后继节点

// Successor 查找给定节点的中序后继
func (r *Node) Successor(n int) *Node {
    // 找到给定节点
    // 如果该节点右边有节点则用FindMini找到后继
    // 如果没有右边节点则后继节点在祖先节点中 在这种情况下 给定节点一定位于中序后继节点也就是祖先节点的左子树中
    // 因为该节点比后继节点小 这个最近的左子树祖父节点就是后继节点
    temp := r.Find(n)
    if temp == nil {
        return temp
    }
    if temp.right != nil {
        return r.Find(temp.right.FindMini())
    } else {
        var successor *Node
        var current = r
        for current.data != n {
            if current.data < n {
                current = current.right
            } else {
                successor = current
                current = current.left
            }
        }
        return successor
    }
}

AVL Tree

一棵AVL树是其每个节点的左子树和右子树的高度差最多为1的二叉查找树。

树的高度为最深叶子节点到该节点层数

为了保证二叉树的平衡， AVL 树引入了所谓监督机制，就是在树的某一部分的不平衡度超过一个阈值后触发相应的平衡操作。保证树的平衡度在可以接受的范围内。具体实现

既然引入了监督机制，我们必然需要一个监督指标，以此来判断是否需要进行平衡操作。这个监督指标被称为“平衡因子（Balance Factor）”。定义如下：

平衡因子： 某个结点的左子树的高度减去右子树的高度得到的差值。

基于平衡因子，我们就可以这样定义 AVL 树。

AVL 树： 所有结点的平衡因子的绝对值都不超过 1 的二叉树。

为了计算平衡因子，我们自然需要在节点中引入高度这一属性。在这里，我们把节点的高度定义为其左右子树的高度的最大值。因此，引入了高度属性的 AVL 树的节点定义如下：

// Node 定义二叉树的节点
type Node struct {
    data  int
    height int
    left  *Node
    right *Node
}

查找二叉树的高度

// FindHeight 查找二叉树的高度
func (r *Node) FindHeight() int {
    // height 指当前节点到最远叶子节点的边数量，叶子节点高度为0
    // depth 指从根节点到当前节点的边数，根节点深度为0
    if r == nil {
        return -1
    }
    // 画图理解
    return max(r.left.FindHeight(), r.right.FindHeight()) + 1
}

计算高度差

// FindHeight 查找二叉树的高度
func (r *Node) TreeGetBalanceFactor() int {
    if r == nil {
        return -1
    }

    return r.left
}